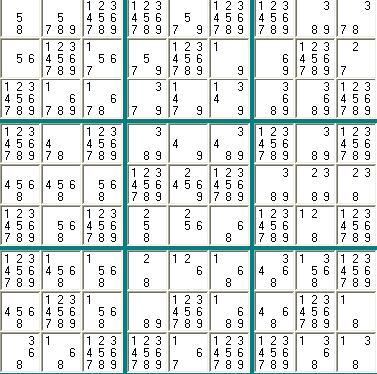
diana ha scritto:. . . seguendo lo stesso procedimento di cancellazione e deduzione logica sono riuscita ad inserire 43 numeri certi.
Ho terminato lo schema a tentativi perchè non sono riuscita a trovare nessuna logica per proseguire.
Se qualcuno ce la fa senza tentativi, mi fa un fischio?
Posso provarci io?
Ho seguito i tuoi passaggi e ricostruito il punto di stallo a cui sei arrivata tu, con 43 Numeri Certi. Dovrebbe essere questo. E’ uno schema un po’ ostico, ma che si presta a varie interessanti riflessioni. Ne faccio qualcuna. Rettangoli Vuoti e Colori Multipli sono parole che potrebbero non dire nulla. Anche perché i Rettangoli sono semmai dei Quadrati. Ed i Colori funzionano benissimo anche in bianco e nero.
Meglio perciò ragionarci sopra.
PRIMA RIFLESSIONE:
- Codice: Seleziona tutto
c1 c2 c3 c4 c5 c6 c7 c8 c9
=============================================================
r1| 58 589 4 | 6 59 2 | 1 3 7 |
r2| 56 3 1567| 579 8 19 |*69 4 2 |
r3| 2 169 167 | 379 -149 34 |*689 *89 5 |
=============================================================
r4| 1 7 2 | 389 49 34 | 5 89 6 |
r5| 4 568 568 | 1 *569 7 |*89 2 3 |
r6| 9 568 3 | 258 256 68 | 7 1 4 |
=============================================================
r7| 7 4 168 | 28 126 168 | 3 5 9 |
r8| 568 2 1568| 89 3 1689 | 4 7 18 |
r9| 3 18 9 | 4 7 5 | 2 6 18 |
=============================================================
Osserva la posizione del candidato 9:
• nel Terzo Riquadro: (celle r2c7–r3c7-r3c8)
• nella Riga 5 (celle r5c5-r5c7)
Nella Colonna 5 il candidato 9 è presente solo due volte:
• se 9 in r5c5: si esclude il 9 da r3c5 (stessa Colonna)
• se 9 in r5c7: si esclude il 9 da r3c5 (nel Terzo Riquadro 9 possibile solo in Riga 3).
Di conseguenza, in ogni caso puoi escludere il 9 da r3c5
SECONDA RIFLESSIONE- Codice: Seleziona tutto
c1 c2 c3 c4 c5 c6 c7 c8 c9
=============================================================
r1| 58 589 4 | 6 59 2 | 1 3 7 |
r2| 56 3 *1567| 579 8 19 | 69 4 2 |
r3| 2 *169 *167 | 379 *149 34 | 689 89 5 |
=============================================================
r4| 1 7 2 | 389 49 34 | 5 89 6 |
r5| 4 568 568 | 1 569 7 | 89 2 3 |
r6| 9 568 3 | 258 256 68 | 7 1 4 |
=============================================================
r7| 7 4 -168 | 28 *126 168 | 3 5 9 |
r8| 568 2 1568| 89 3 1689 | 4 7 18 |
r9| 3 18 9 | 4 7 5 | 2 6 18 |
=============================================================
Con un ragionamento analogo a quello del caso precedente, puoi escludere il candidato 1 da r7c3
TERZA RIFLESSIONEdiana ha scritto:. . . purtroppo i rettangoli vuoti mi restano proprio indigesti . .
Nadia
- Codice: Seleziona tutto
c1 c2 c3 c4 c5 c6 c7 c8 c9
=============================================================
r1| 58 589 4 | 6 59 2 | 1 3 7 |
r2| 56 3 a1567| 579 8 *19 | 69 4 2 |
r3| 2 b169 c67 | 379 *149 34 | 689 89 5 |
=============================================================
r4| 1 7 2 | 389 49 34 | 5 89 6 |
r5| 4 568 568 | 1 569 7 | 89 2 3 |
r6| 9 568 3 | 258 256 68 | 7 1 4 |
=============================================================
r7| 7 4 -168 | 28 *126 168 | 3 5 9 |
r8| 568 2 1568| 89 3 1689 | 4 7 18 |
r9| 3 *18 9 | 4 7 5 | 2 6 18 |
=============================================================
Alla esclusione del candidato 1 da r7c3 ci si può arrivare anche per altro modo. Certamente più difficile e lungo a descrivere che non a mettere in pratica.
Il candidato 1 è sicuramente Numero Certo di almeno una di queste due celle:
• cella r7c5
• cella r9c2.
Di conseguenza un candidato 1 presente in una cella che si trovi nella stessa Sezione sia dell’una che dell’altra di queste due celle deve essere escluso.
E’ appunto il caso dell’1 nella cella r7c3 che è:
• sulla stessa Riga della cella r7c5
• nello stesso Riquadro della cella r9c2
Perché il candidato 1 è sicuramente Numero Certo di almeno una delle celle r7c5 e r9c2?
Osserviamo il candidato 1 nel Primo Riquadro.
Esso è presente tre volte, e precisamente nelle celle:
r2c3 – che chiamiamo a
r3c2 – che chiamiamo b
r3c3 – che chiamiamo c
Queste le tre possibilità:
PRIMA POSSIBILITA’
1 Numero Certo di a (r2c3).
In tal caso:
• 1 assente in b (r3c2) (stesso Riquadro)
• 1 Numero Certo di r9c2 (unico nella Colonna 2)
SECONDA POSSIBILITA’ 3 Numero Certo di c (r3c3).
Lo scenario è identico a quello del caso precedente:
• 1 assente in b (r3c2) (stesso Riquadro)
• 1 Numero Certo di r9c2 (unico nella Colonna 2)
TERZA POSSIBILITA’1 Numero Certo di b (r2c3).
In tal caso:
• 1 assente in a (r3c2) (stesso Riquadro)
• 1 Numero Certo di r2c6 (unico nella Riga 2)
• 1 assente in r3c5 (stesso Riquadro)
• 1 Numero Certo di r7c5 (unico nella Colonna 5)
In ogni caso, quindi, quale che sia la collocazione del candidato 1 nel primo Riquadro, lo stesso 1 sarà Numero Certo di almeno una delle due celle r7c5 e r9c2.
E quindi va escluso da r7c3, come si diceva.
Con queste operazioni (in parte riprese da Amalia nel suo intervento) lo schema si apre, ma non si risolve. E’ necessario fare qualche altro passo, ma mi fermo qui per non risultare ancora più noioso.
Considerazioni di questo tipo sono molto meno complesse di quanto possano sembrare in un primo momento: dopo aver assimilato il concetto di fondo, basta solo un po’ di esercizio per affinare il colpo d’occhio.
Certo, si fa molto prima con i tentativi (specie se ragionati). Ma questa è tutta un’altra logica.
Un caro saluto a te e a tutti.
Paolo
P.S. Ho una immagine dei tuoi occhi sbarrati durante le faticose prove di Lucca. La foto, presa da un telefonino da quattro soldi, non è di grande qualità. Ma l’espressione (come avevo tentato di descrivere a tuo marito) è di straordinaria eloquenza e di eccellente fattura. Te la mando. . . anche perché sei con quel bell’uomo del tuo compagno di banco (o di banca?). Se solo mi prometti che la prossima volta trascrivi anche lo schema. . .per ricostruirlo sono davvero ammattito.