Patchwork- Guida alla risoluzione
Ok, Gabriele, ci penso io 
Prendiamo il patchwork facile del 9 giugno (quello ancora pubblicato). I numeri in nero sono quelli dati dallo schema, quelli in blu sono i candidati (e i numeri certi) inseriti da noi. Dato che come dimensioni è simile a un classico sudoku 9x9, dividiamolo in 9 "righe" e 9 "colonne" per comodità di spiegazione. Le strategie le dò nel "mio" ordine, ma ognuno risolvendo può usarle nell'ordine che vuole
In questo caso i numeri certi possibili sono l'1, il 2 e il 3.
Potete ingrandire le immagini cliccandoci su e aprendole in una pagina nuova.
1) AFFIANCAMENTO:
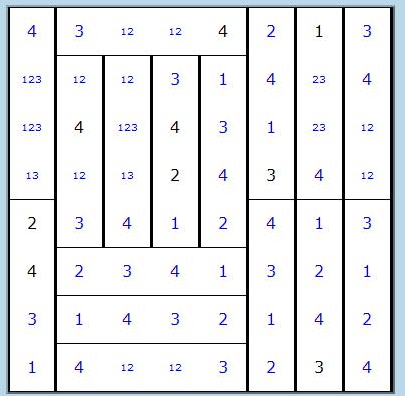
Nessun numero certo può affiancare in orizzontale o in verticale un numero uguale. Quindi scriviamo i due candidati restanti ai lati di ciascun numero certo. Se una casella è affiancata da due numeri certi diversi tra loro (come la r2c5, fiancheggiata dall'1 e il 3), si può inserire il terzo (il 2) e i relativi candidati ai lati.
Otteniamo questo:
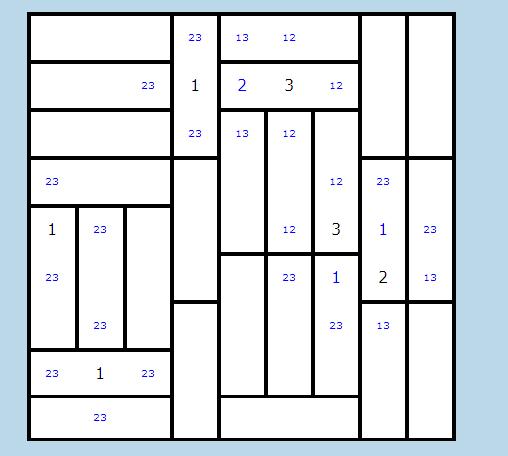

2) COMPLETAMENTO SETTORI (E AFFIANCAMENTO)
Ogni settore da 3 deve contenere i tre numeri diversi tra loro. Inseriamo i nuovi candidati tenendo conto contemporaneamente della regola 1 (MAI dimenticare i passi precedenti! ). Otterremo questo:
). Otterremo questo:
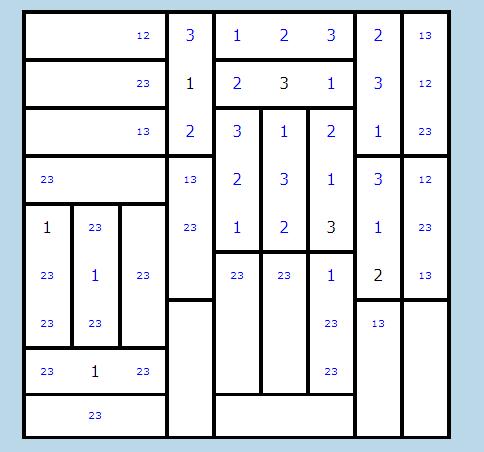

3) OSSERVAZIONE DELLE RIGHE:
Ogni riga deve contenere esattamente 3 volte l'1, il 2 e il 3 (visto che si tratta di uno schema a 9 caselle con 3 candidati).
Quindi, ad esempio:
- se un numero è già piazzato 3 volte, nelle restanti caselle incerte andrà escluso dai candidati;
- se una riga contiene 2 settori orizzontali, le caselle restanti dovranno avere numeri diversi tra loro. Guardiamo ad esempio la riga 1 nell'immagine SOPRA: in r1c9 i candidati sono 1 e 3, ma, escludendo i due settori orizzontali, il 3 è già presente. Quindi in r1c9 andrà l'1, e per la regola 1 in r2c9 andrà il 2, e via così.
Lo stesso, ad esempio, in riga 4, colonna 4, candidato 3: considerando anche il settore orizzontale che conterrà il numero 3, il 3 è già presente 3 volte. Quindi andrà escluso da r4c4, dove andrà l'1.
Il risultato è questo:
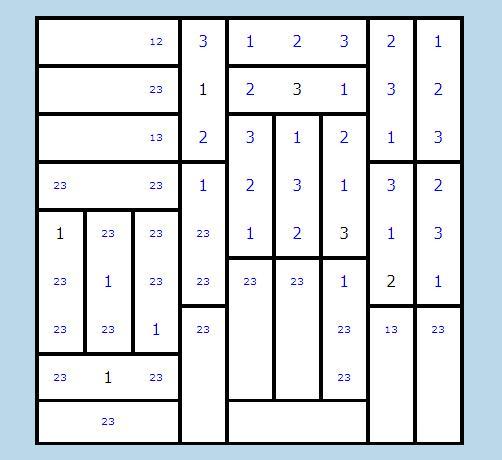

4. OSSERVAZIONE COLONNE
Facciamo lo stesso per le colonne. Guardando l'immagine precedente, si nota subito che ad esempio in r9c5 deve stare per forza il 3, in r9c6 l'1 e così via.
Otteniamo questo:
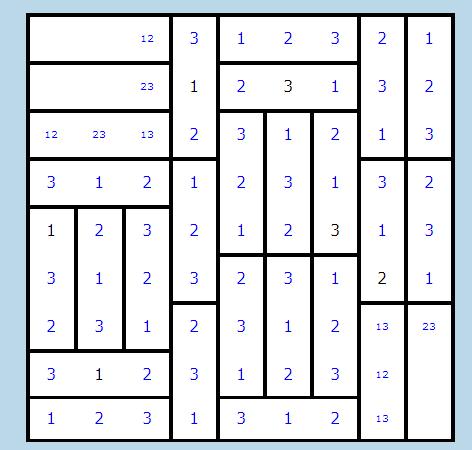

5. COMPLETAMENTO
A questo punto, tenendo conto dei candidati presenti e del fatto che in ogni riga e in ogni colonna ogni numero va ripetuto esattamente 3 volte, è facile completare.
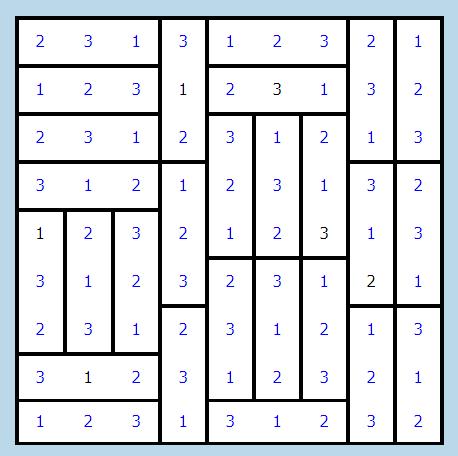

Spero di essere stata chiara...altrimenti chiedete pure
Prendiamo il patchwork facile del 9 giugno (quello ancora pubblicato). I numeri in nero sono quelli dati dallo schema, quelli in blu sono i candidati (e i numeri certi) inseriti da noi. Dato che come dimensioni è simile a un classico sudoku 9x9, dividiamolo in 9 "righe" e 9 "colonne" per comodità di spiegazione. Le strategie le dò nel "mio" ordine, ma ognuno risolvendo può usarle nell'ordine che vuole
In questo caso i numeri certi possibili sono l'1, il 2 e il 3.
Potete ingrandire le immagini cliccandoci su e aprendole in una pagina nuova.
1) AFFIANCAMENTO:
Nessun numero certo può affiancare in orizzontale o in verticale un numero uguale. Quindi scriviamo i due candidati restanti ai lati di ciascun numero certo. Se una casella è affiancata da due numeri certi diversi tra loro (come la r2c5, fiancheggiata dall'1 e il 3), si può inserire il terzo (il 2) e i relativi candidati ai lati.
Otteniamo questo:


2) COMPLETAMENTO SETTORI (E AFFIANCAMENTO)
Ogni settore da 3 deve contenere i tre numeri diversi tra loro. Inseriamo i nuovi candidati tenendo conto contemporaneamente della regola 1 (MAI dimenticare i passi precedenti!
 ). Otterremo questo:
). Otterremo questo:

3) OSSERVAZIONE DELLE RIGHE:
Ogni riga deve contenere esattamente 3 volte l'1, il 2 e il 3 (visto che si tratta di uno schema a 9 caselle con 3 candidati).
Quindi, ad esempio:
- se un numero è già piazzato 3 volte, nelle restanti caselle incerte andrà escluso dai candidati;
- se una riga contiene 2 settori orizzontali, le caselle restanti dovranno avere numeri diversi tra loro. Guardiamo ad esempio la riga 1 nell'immagine SOPRA: in r1c9 i candidati sono 1 e 3, ma, escludendo i due settori orizzontali, il 3 è già presente. Quindi in r1c9 andrà l'1, e per la regola 1 in r2c9 andrà il 2, e via così.
Lo stesso, ad esempio, in riga 4, colonna 4, candidato 3: considerando anche il settore orizzontale che conterrà il numero 3, il 3 è già presente 3 volte. Quindi andrà escluso da r4c4, dove andrà l'1.
Il risultato è questo:


4. OSSERVAZIONE COLONNE
Facciamo lo stesso per le colonne. Guardando l'immagine precedente, si nota subito che ad esempio in r9c5 deve stare per forza il 3, in r9c6 l'1 e così via.
Otteniamo questo:


5. COMPLETAMENTO
A questo punto, tenendo conto dei candidati presenti e del fatto che in ogni riga e in ogni colonna ogni numero va ripetuto esattamente 3 volte, è facile completare.


Spero di essere stata chiara...altrimenti chiedete pure